Prime number theorem

Statement of the prime number theory:

Let π(x) be the prime - counting function that gives the cardinal of primes which is less than or equal to x, for any absolute cardinal x. For example, π(10) = 4 because 2, 3, 5 and 7 are prime numbers which are less than or equal to 10.

According to prime number theorem,the limit of the quotient of the two functions π(x) and x / ln(x) as x approaches infinity is 1, which is expressed by the formula:

Using asymptotic notation the above formula can be written as

 

The theorem states that x/ln(x) approximates π(x) which means that the relative error of this approximation approaches 0 as x approaches infinity.

See the link for Prime and composite numbers

An example of the problem on prime number theory is given below: 

 

Solution:

 

Parallel lines

Definition of parallel lines: Two lines are said to be parallel if they never meet each other.Two parallel lines are always apart by the same distance.

There is a link provided below where you will learn in detail about parallel lines:parallel perpendicular lines

The diagram of of parallel lines are shown below:

Properties of parallel lines:
1)When another line is drawn through two or more parallel lines, The resulting angles are same.
2)The sum of the two adjacent angles is 180 degree

I am giving a link on Pair of straight lines as well.

Next time we will learn the above properties with the help of diagram by giving detail explanation.      

Binomial theorem

Binomial Theorem:

According to Binomial theorem, it is possible to expand any power of x + y into a sum of the for

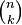where indicates the corresponding binomial coefficient.By using the summation notation ,the above formula can be written as

A variant of the binomial formula is obtained by substituting  1 for x and x for y, so that it involves only a single variable. In this form, the formula reads

See the given link on how to solve problem on binomial theorem.I hope this blog on the binomial theorem will give you the basic knowledge to solve problem on binomial problems

Intersection

Two lines intersect each other if they cut each other at one point.We can also find the point of intersection of two lines.A line may be indicated by the function f(x) = 5x + 3.Where the two lines cross is called the point of intersection.There are different ways to find the point of intersection of two lines.

Not only lines intersect, but even curves can intersect each other.They can intersect at more than two points as well.You may see the given link for finding angle of intersection between Curves.

Get help on procedure to find angle of intersection of two curves.

Intersection may take place between planes, circles, spheres, etc.You will understand the meaning of intersection with the help of diagrams.

                                       

Quadrilateral

Quadrilaterals are any shapes which have four sides of straight lines.For example, parallelogram is a quadrilateral.Quadrilateral are 2-dimensional shapes.

There are different types of quadrilaterals.Square, rectangle and rhombus are different types of quadrilaterals.All the sides of square have equal length.In rectangle, two opposite sides have equal length.The sides of rhombus are of different length.

How to calculate the area of a quadrilateral?
There are different formula of quadrilaterals according the the types of the quadrilateral.You can see the given link to know how to calculate the area of quadrilateral.

The parts of a quadrilateral include its angles, sides and diagonals.A diagonal of a quadrilateral is a straight line joining the opposite vertices.The perimeter of a quadrilateral is the sum of the length of its sides.

Geometry problems

As you know geometry deals with shapes and their properties.So, in order to solve geometry problems you need to memorize the basic formula of all the shape.

Example of geometry problem:
In geometry, problem may be given to find the area of a triangle.The formulae of the area of a triangle is given as A = 1/2 b x h, where b is the adjacent and h is the opposite of the triangle.If the b is 3cm and h is 8cm, then according to the formulae, A = 1/2 x 3 x 8 = 24/2 = 12 sq.cm.

Similarly, geometry problems will need formula for solving.
You can practice geometry problems by referring to solved geometry problems.
Solved geometry problems is available in the form of books by experts or you will also get from websites.

Geometry help

In geometry, we learn about shapes and their properties.Geometry is classified into two types:One deals with two dimensional shape i.e, plane geometry and the other one deals with 3-dimensional shape i.e, solid geometry.

Free geometry help is available online from different online tutoring company who have experienced expert tutors.Teachings are given for both beginners and advanced students.

You can avail free online geometry tutor to check whether you are satisfied with the teaching style.This free tutoring is given so that you will have the knowledge of effectivenes.

Studying the shapes of triangle, parallelogram, circle, etc. and their properties is included in geometry.

Fraction

What is a fraction?
A fraction is a part of a whole.A fraction is represented by a number having numerator and denominator.For example, 2/8 is a fraction.

How to divide fractions?
Suppose (3/4)/(4/2) is given ,
Convert the divisor into multiplication and invert the denominator.Then we get,

3/4 x 2/4 = 6/16 = 3/8.

How to add fractions? Fractions can be added by following the steps given below:
1)Make sure that the denominators are same.
2)Add the numerators
3)Put the answer on the same denominators and simplify if needed.

Adding fractions example: Let 1/4 + 2/4 be the given for addition.
According to the first step,since the denominators are same , the numerators will be added, we get
(1+2)/4 = 3/4
So the answer is 3/4.

understang the terms in circle

Basic terms of circles:

Center of the circle:In geometry circles, the fixed point , the fixed point is called the center of the circle.

Radius of a circle:The distance from the fixed point to any point on the circumference of the circle is called the radius.

Concentric circles:Concentric circles are circles drawn from a fixed point.

Chord: A chord is a line that is formed by joining two line of an arc.

Diameter: A diameter is a chord passing through the center of the circle.

I hope this basic terms will be of helpful ones.

Segment of a circle

Segment of a circle: When a chord divides the circle into two regions, the two regions are called circle segments.

There are major and minor segments.The major segment is the region bounded by the chord  and the major arc intercepted by the chord. The minor segment is the region bounded by the chord and the minor arc intercepted by the chord.

Circle segment area:The area of the segment of a circle is equal to the the area of the circular sector minus the area of the triangular portion.

The formula of the area of the circle segment is given as:

½ × ( (θ × π/180) - sin θ) × r²   (if θ is in degrees)
 

Types of circle

A circle is the locus of all points which are at a fixed distance from a fixed point.There are two kinds of circles - tangent circle and intersecting circle.

Tangent circles: A tangent circle is a circle on which a line is drawn by touching at a point of the circumference of the circle.
Intersecting circles:When two circles intersect at two points it is called an intersecting circles.

Circle properties:1)Circles which have same radii are congruent
                           2)Equal circles have equal circumference.

There are many more properties of circles which we will discuss next time with diagrams.

Learn elementary statistics

What is statistics?
Statistics is the science of the collection, organization and interpretation of data.

Elementary statistics.
In the elementary statistics, you will learn the basic concepts in statistics such as the basic topics included in
statistics.Basic statistics include find the mean, mode and median.Here is an example of calculating the mean value.
Let us find the mean value of 4, 8, 2 and 10
First add the numbers as 4+8+2+10 = 24
Divide the value that you got by addition of the numbers by number of the numbers i.e, 4
Then, 24/4 = 6
So, the mean value is 6.

Next time we will learn how to find the mode and median.

Square number

Square of a number is the number that you get when you multiply a number with itself .For example, 16 is the square number of 4.

How to find the square of a number?
1)Take any number you want to square
2)Take the number before and after the number you have chosen to find its square
3)Multiply both the numbers that are before and after the number.
4)Add 1 to the number you got on multiplying.Now you will get the square of the number.

Suppose you want to find the square of the number 9
The number before 9 is 8 and the number after 9 is 10
Now, multiply 8 and 10.We know that 8 x 10 is 80
Add 1 to 80, then we get 81. So, 81 is the square of 9.

Hope you will find this article helpful.
Do post comments.

Area of a triangle

A triangle is a polygon with three corners or vertices and three sides which are line segments.A triangle with three vertices A, B and C are written as ABC .


Let's see how to calculate the area of a triangle.
Area of a triangle formula is given as:
1/2b x h , where b is the base and h is the height of the triangle.


Let us take an example. Suppose, we have a ABC whose base is 3cm, height - 5cm, 
then, by using the formula Area of a triangle = 1/2b x h ,

we can write Area of the triangle = 1/2 x 3 x 5 = 15/2 = 7.5 sq.unit.

There are different ways to calculate the area of a triangle according to the types of triangle.We will learn 
the different ways next time.